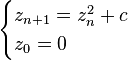マンデルブロ集合を描画しよう
プログラマというものはフラクタルが好きというのは至極当然の話です。
マンデルブロ集合、シェルピンスキーのギャスケット、コッホ曲線、etc、・・・。フラクタル系の図形は色々あります。でも自前でフラクタルを描画したことがある人って意外と少ないのではないでしょうか。今回、Java と gnuplot を用いてマンデルブロ集合を描画してみましょう。
マンデルブロ集合とは
Wikipedia によると、
で定義される複素数列 {zn}n∈N が n → ∞ の極限で無限大に発散しないという条件を満たす複素数 c 全体が作る集合がマンデルブロ集合である。
とのことです。
式
ではまず例の式を Java コードに落としてみましょう。
興味があるのは無限大に発散するか否かなので、適当にループ回数と閾値を決めて、閾値を超えたら無限大に発散する、という判定を組み込むことにします。ループ回数の最大値は 1000 。z.abs() が 10 を超えたら無限大に発散するということにしましょう。一見少なく見えますが、手元であれこれ実験した感じだとこの閾値で十分でした。
private static boolean mandelbrot(Complex c) { Complex z = Complex.ZERO; int i = 0; for (i = 0; i < 1000; i++) { z = z.multiply(z).add(c); if (z.abs() > 10) { return true; } } return false; }
2 次元プロット
では上記 mandelbrot 関数を用いて、無限に発散した点のみプロットしてみましょう。
public static void main(String[] args) throws IOException { double diff = 0.005; try (FileWriter writer = new FileWriter("/tmp/mandelbrot/data.dat")) { for (double r = -2; r < 1; r += diff) { for (double i = -1; i < 1; i += diff) { boolean diverge = mandelbrot(new Complex(r, i)); if (!diverge) { writer.write(r + "\t" + i + "\n"); } } } } }
これを実行して得た data.dat を gnuplot に食わせて、
plot 'data.dat' w d
を行うと・・・
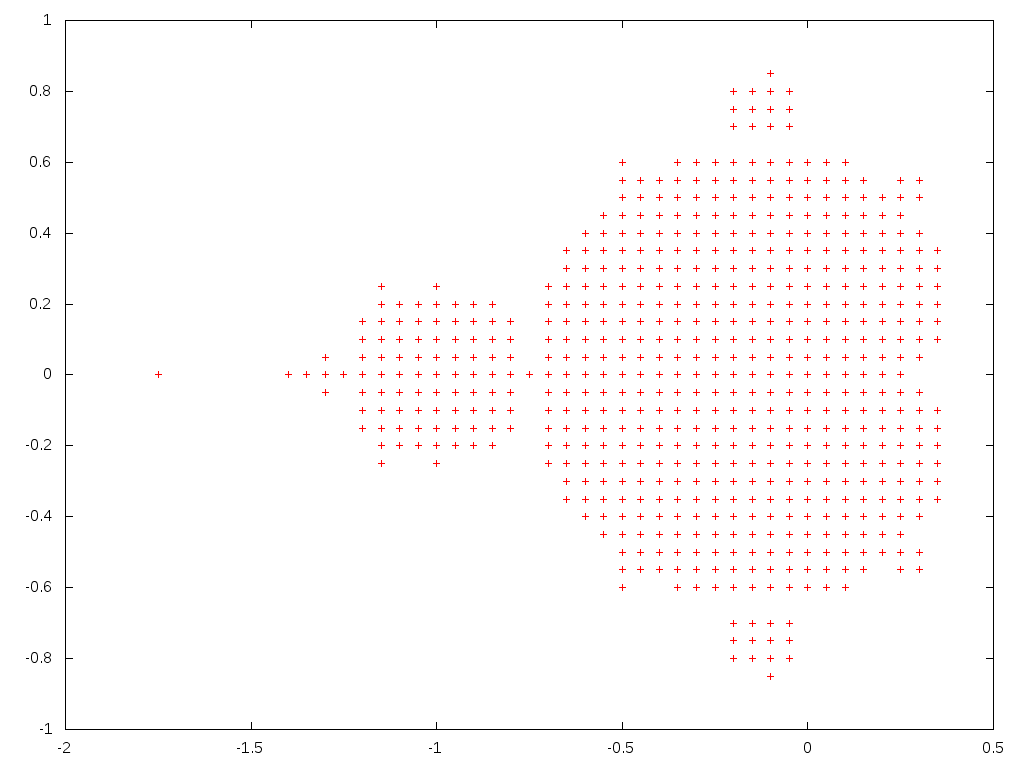
おお!ぼんやりとマンデルブロ集合が見えますね!
でもちょっと粒度が粗いので、もう少し細かくしてプロットしてみましょう。
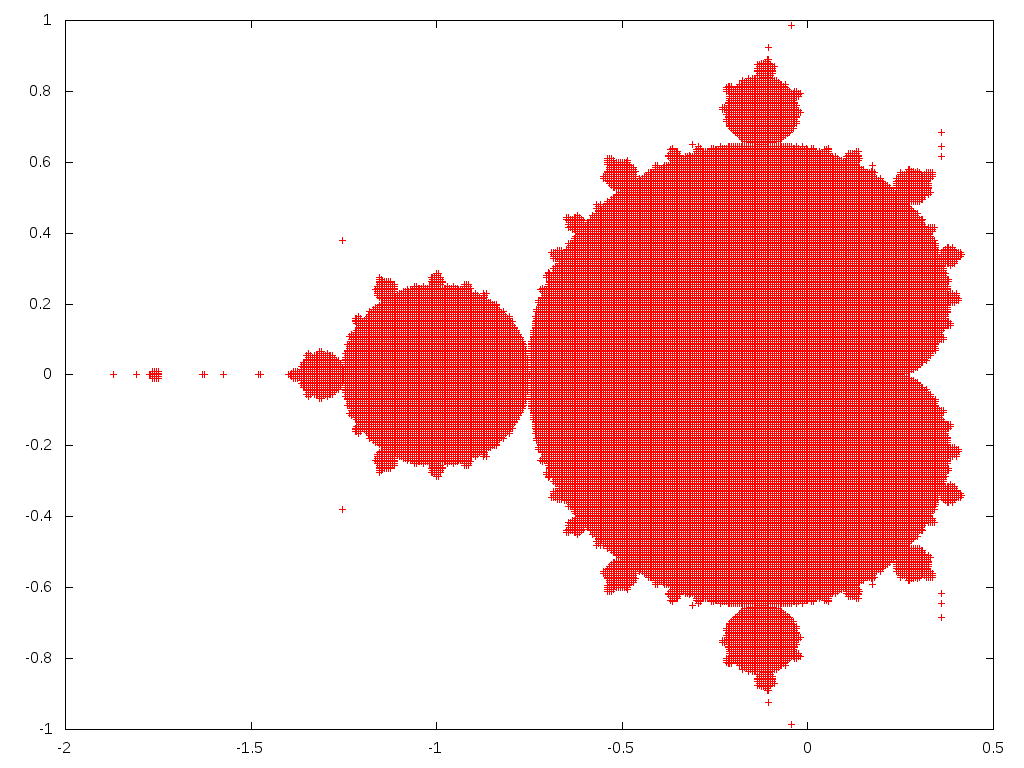
かなりマンデルブロ集合っぽくなりました。
3 次元プロット
さて色付けするために、z 軸の要素に発散するまでの回数を入れてみます。
コードはこんな感じ。
public static int mandelbrotCount(Complex c) { Complex z = Complex.ZERO; int i = 0; for (i = 0; i < 100; i++) { z = z.multiply(z).add(c); if (z.abs() > 10) { break; } } return i; } public static void main(String[] args) throws IOException { double diff = 0.001; try (FileWriter writer = new FileWriter("/tmp/mandelbrot/data.dat")) { for (double r = -2; r < 1; r += diff) { for (double i = -1; i < 1; i += diff) { double value = mandelbrotCount(new Complex(r, i)); if (value > 0) writer.write(r + "\t" + i + "\t" + value + "\n"); } writer.write("\n"); } } }
出てきた data.dat をこんな感じで plot します。
set terminal png size 1024,768 set output 'mandelbrot.png' set hidden3d set logscale z splot 'data.dat'
すると・・・
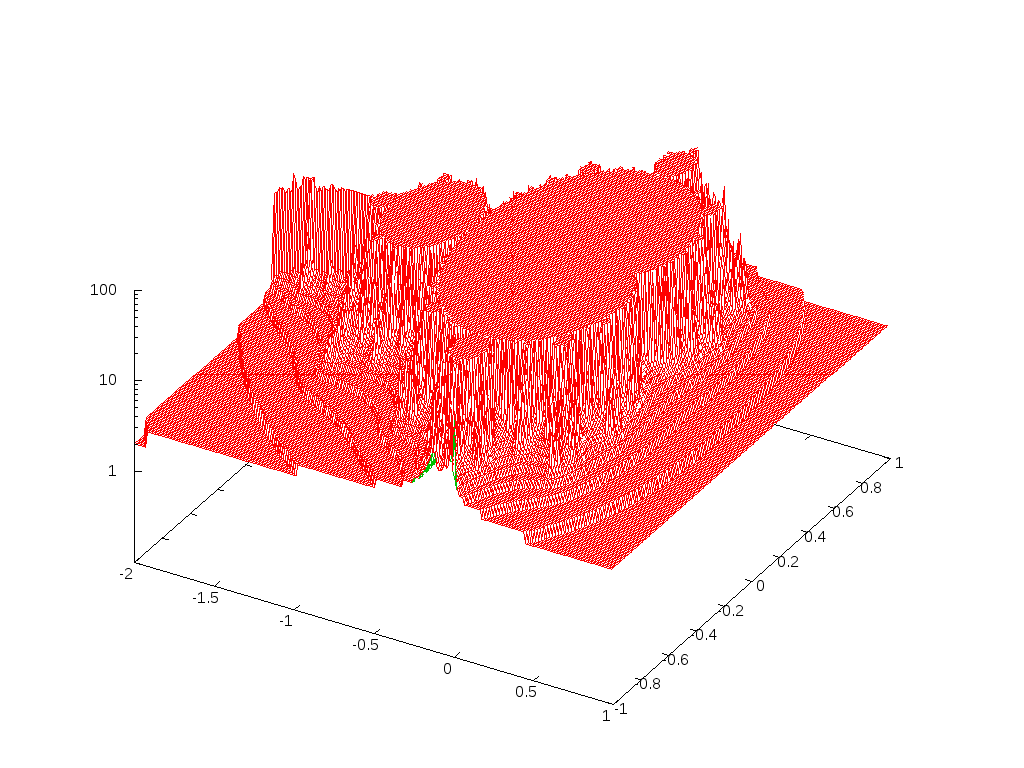
来てますね!
最後に、pm3d 使って色付けしてみましょう。
set pm3d set pm3d map set palette defined(0"#000099",1"#ffffff",2"black") set terminal png size 1024,768 set output 'mandelbrot-pm3d.png' splot 'data.dat' notitle
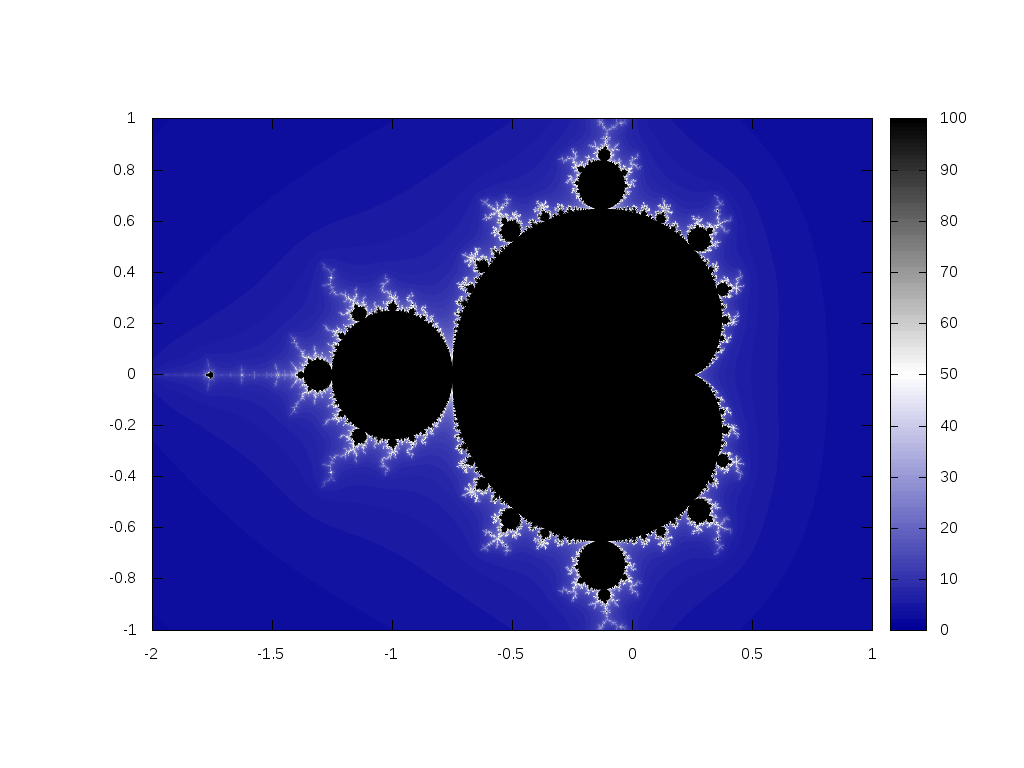
カッコイイ!Wikipedia にあるものと比べてそれほど遜色ないはず!
というわけで、マンデルブロ集合は簡単にプロットできたのでした。めでたしめでたし。

- 作者: 三井秀樹
- 出版社/メーカー: 中央公論社
- 発売日: 1996/04/25
- メディア: 新書
- 購入: 10人 クリック: 70回
- この商品を含むブログ (27件) を見る